The Magic of Emergence

New concepts arise when the right parts align

When you put things together in the right way, magic happens.

If I put some words together in the right order here, they will form a coherent article. That article could have different properties than any individual word, properties like "causes amusement", "teaches you things", and "makes you give me the respect I so desperately seek".

Sometimes when we put something together, the emergent properties are so interesting, it enriches our concepts of the world.

By arranging long pieces of metal (wire) and connecting them to machines that generate a flow of tiny particles (electrons) we create emergent properties so unique and useful it becomes its own concept: electricity. 

The emergent concept takes on a life of its own, becoming something to be studied and built on top of. Our ontology becomes enriched. We open up new conceptual landscapes to explore.

Similarly, when we combine the right parts, we get something that has shaped the modern world and the modern conceptual landscape: computers.

But those machines in their modern form only came about through multiple conceptual leaps.

Computers

Before the current age where we all have supercomputers in our pockets, computation was a valuable, scarce resource.

Military operations require a lot of computation. You have to figure out things like where to point your artillery so the shells explode the right people. You might also want to break the encryption codes of your enemy so you can understand any communications you intercept.

Back around the time of the second world war, the military would build big computational machines to solve these specific problems. For example, differential analyzers were big complex machines capable of solving certain differential equations. The military used these to compute artillery trajectory tables to be used in the field.

These big differential analyzers were basically specialized calculators. They could solve a specific class of math problem, but they weren't the computers we know today. You set up one specific equation, and they could crank through it and spit out a number. It was more like a big automated abacus.

It lacked the flexibility of modern computers to have branching logic. Not only was this annoying, but this lack of flexibility meant there were types of equations that the differential analyzers weren't equipped to solve.

Differential analyzers were one example of early computational devices—history is full of other special-made machines for solving specific math problems.

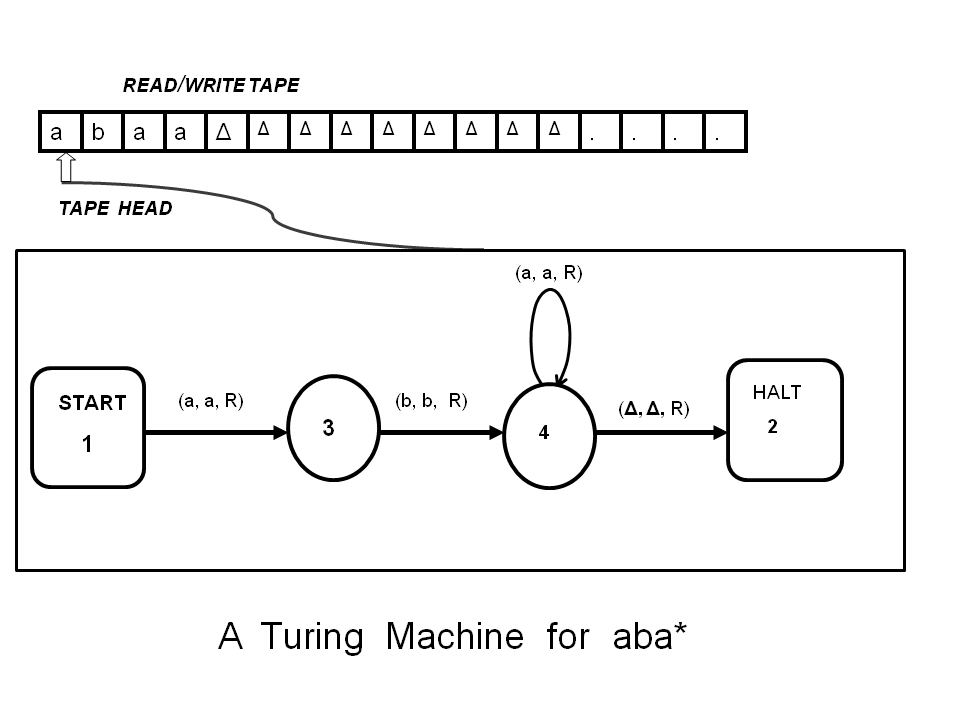
Alan Turing wanted to find the limits of what a computational machine could do. In a now-legendary paper, he introduced the idea of a universal computing machine (later called a Turing Machine).

Turing's universal computing machine is an abstract concept. It's an imagined machine that performs operations on a tape with symbols. The head of the machine can read the symbols on the tape, and act based on a combination of those symbols, a table of rules, and a set of states the machine can be in. The head then can perform actions like replacing the current symbol on the tape, or moving the tape left or right to the next symbol.

An example Turing Machine.

Turing Machines were conceptually new, but they were an extremely powerful idea. Despite being extremely simple in their specification, a special property comes out of these components working together: universal computability. It is generally believed a function is only computable if it can be computed by a Turing Machine (interestingly, this is mathematically unproven, but is taken as true in computer science).

In other words, if a Turing Machine can't be specified to solve a computational problem, it can't be solved by any machine.

This conceptual shift from specialized devices for each type of computation to a single device that could do any computation is profound. By thinking of a machine with the right kind of flexibility, we could make the leap from mere calculators to computers capable of the computation we can do today.

But the Turing machine was just a mathematical concept. We still had to figure out how to build them.

Lovelace, Babbage, and Taking Computation Beyond Math

A century before Turing came up with the concept of the Turing machine, Charles Babbage had almost made one a reality.

While working on a more specialized "difference engine" (again, essentially a specialized calculator), Babbage had an insight similar to Turing's: a more generalizable computing device. He designed his Analytical Engine without the theoretical framework of Turing machines, but the Analytical Engine is "Turing-Complete"—the term for something capable of any computation a Turing machine could do. It could, in principle, perform any calculation any future computer could.

And he had the designs to make one a reality.

Sadly, the Analytical Engine wasn't built in Babbage's lifetime. Potential funders were spooked by the enormous cost of constructing such a thing and the uncertainty about if it would actually work.

The person to best recognize the potential of the Analytical Engine wasn't Babbage, but his close collaborator, the mathematician Ada Lovelace. Lovelace is considered by some to be the first computer programmer for her work on the Analytical Engine. She was also the first to recognize that a universal computer like the Analytical Engine could be used for more than just solving math equations.

Lovelace recognized that such a flexible machine could manipulate symbols to perform any task that could be broken down into logical steps. She wrote about it being used for musical composition or other artistic endeavors. She saw the Analytical Engine in a surprisingly modern way: it wasn't a mere math machine; it performed symbolic processing.

Lovelace recognized Turing-Complete computers weren't just more powerful calculators. Something new emerged from their flexibility. It seems obvious to us now that they aren't just big calculators since we use them to play video games or write blog articles. But this was a huge conceptual leap.

It took the world a long time to catch up to Lovelace's leap.

The Architect

A century after Lovelace and Babbage, and a few years after Turing's paper, the US Department of Defense was pouring money into computation. 

The army needed more math so they could fight the Nazis. They wanted to compute their ballistics tables (and later, see how big a boom nuclear bombs would make).

The design of such a complex machine using fancy new technology like vacuum tubes was a huge challenge—the final ENIAC machine had tens of thousands of vacuum tubes, resistors, and capacitors. It would be the machine that calculated the yield of the hydrogen bomb. To architect such a thing they needed a genius.

Enter John von Neumann.

Reading anecdotes about him, von Neumann seems like a mythical creature. His mathematical prowess was astounding and he seemed to be involved in every technical problem of his age. He wrote the founding papers in multiple areas of mathematics, quantum physics, and fluid dynamics. While he was at it he founded game theory. His thoughts were considered so valuable that in 1947, the RAND corporation paid him $200 a month (over $2,500 in today's dollars) to just think about their problems during the time he spent shaving.

Von Neumann got involved in the computer-designing fun. A product of one of those efforts (the EDVAC project) was the von Neumann architecture, which is the basis of nearly all modern computers.

Simplified von Neumann architecture. Image source.

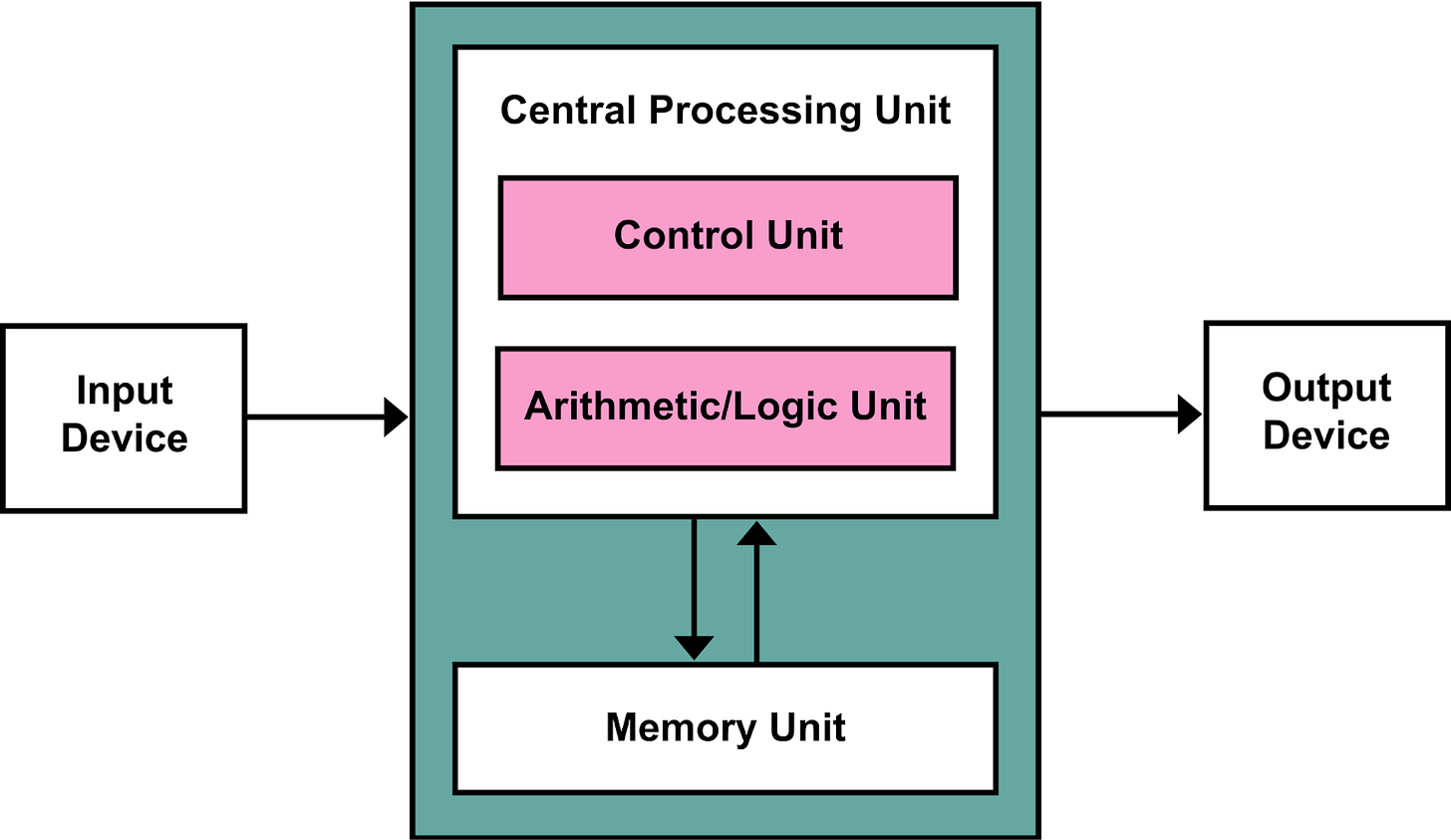
One important concept of the von Neumann architecture was the idea of a stored-program computer. The memory the computer uses to store data is the same memory that stores the instructions (or program) the computer will carry out.

This idea wasn't original to John von Neumann—the seeds were already in Turing's famous paper, and Turing himself proposed a stored-program architecture to the British government around the same time.

But regardless of where credit was due, the stored-program concept was an important reconceptualization in computational history. Instructions were just data. No need to physically reconfigure anything to get a machine to do what you wanted, moving plugs and flipping switches.

This reconceptualization isn't just one of convenience. If code is just data, code can act on code.

This led to many of the tools that bootstrapped the environment for software development we have today, like assemblers and compilers. This conceptual shift not only gave us the most practical way to bring a Turing Machine to life, but also allowed programming languages to become as flexible and abstract as they are today.

One-Shot Problems to Interaction

With the creation of the first big Turing-Complete computers like the ENIAC, computers were still being treated as big, flexible calculators. You gave them a bunch of numbers to calculate, and then stepped back and let it crunch through those numbers.

This is called batch processing (and is still often done in computer systems). There's no interaction, just a pile of problems for the computer to work through.

They were being used for a wider range of tasks, and universities were opening them up to use by professors and students. If you know someone who took any computer classes in the 1960s, they probably have stories about submitting punch cards to the computer, and only discovering the output hours—or even days—later.

The problems with this situation were well understood—it sucked to wait days to run your program, only to learn there was something wrong with the code you wrote.

Even though these problems were well-understood, universities were reluctant to give computer users blocks of dedicated time on the computer. Computers were so expensive, any time it sat idle was a big cost. It was more efficient to queue up jobs from everyone and have the computer constantly chugging through a pile of jobs. Waiting for one user to input their code and see the output would have resulted in a lot of expensive dead time.

Two solutions emerged. One was the idea of time-sharing, where a big expensive computer could have its time split between multiple users having an interactive session at the same time. This would cut down on the amount of dead-time the computer had, and since the computers were so quick by that time they could seamlessly switch between the instructions of multiple users while still giving feedback to each.

The other solution was simply smaller, cheaper machines designed for interactive computing. The PDP-1 sold for a cheap $120,000 (over $1,000,000 in today's dollars) and was tiny, weighing only 1600 lbs. MIT would let employees and students use such a cheap machine for dedicated interactive sessions.

Up until that point, using a computer meant either being a programmer or being trained in special software that would allow you to input numbers and calculate a result. The experience we associate with computers nowadays—you click a button and something happens immediately—was a foreign concept.

But once a wide set of users started having dedicated time, magic happened. People started creating interactive computer programs designed for non-specialized users. 

For example, at MIT, users of the PDP-1 created the first—or at least, most influential—interactive computer programs. Along with a bunch of other interactive programs, the influential Spacewar! video game was born.

The idea of using this complex machinery originally designed for crunching numbers for ballistics tables to play a game was a conceptual leap. You didn't just give the computer a pile of instructions or numbers and wait for it to crunch through—the computer responded to a single button press immediately, and this opened the door to qualitatively different experiences. 

Conceptual Shifts and the Magic of Emergence

Putting things together in the right ways can summon mystical creatures from the ether, like von Neumann's architecture animating the abstract idea of Turing's Universal Computing Machine.

Taking these colossal calculators and reconceptualizing what they could do—from math to symbol processing, from solving pre-defined problems to providing interactive experiences—changed the world. New conceptual landscapes have emerged from the qualitatively different ways we interact with computers.

Our modern interactive computing experiences are emergent properties built on emergent properties. Each new emerging power opened a doorway that we explored, and those explorations led to new emergent properties.

We've learned how to build computers, and so too have we built up our ontology of the world. We're goddamn wizards, but even more amazing is that the mystical powers we have are understandable. We don't have computers "just because". We can break them down into understandable pieces and it's comprehensible to us how the parts become the whole.

That's the real magic.

---

Please hit the ❤️ “Like” button below if you enjoyed this post, it helps others find this article.

If you enjoy the newsletter, consider upgrading to a paid subscriber to support my writing.

If you’re a Substack writer and have been enjoying Cognitive Wonderland, consider adding it to your recommendations. I really appreciate the support.