The Unreasonable Effectiveness of the Obvious
Power laws, Buridan's Ass, and not fretting the small stuff
Please hit the ❤️ “Like” button at the top or bottom of this article if you enjoy it. It helps others find it.
In linguistics, there's a funny observation: if you order words by how frequently they appear, there is a steep decline in frequencies. The most common words appear a ridiculous amount, and this drops off quickly.
For example, in a common English corpus (the Brown Corpus), the word "the" is the most frequent word, accounting for 7% of all words. The second-most frequent word, "of", accounts for 3.5% of words—roughly half as frequently as the most common word.
It turns out this is a general pattern: the nth word appears roughly 1/n times in most texts—this is called Zipf's law. More generally, word frequencies follow an inverse power law.
An inverse power law is a relationship between two variables (the rank of a word and its frequency) that displays an initial steep drop-off, followed by a tapering off.
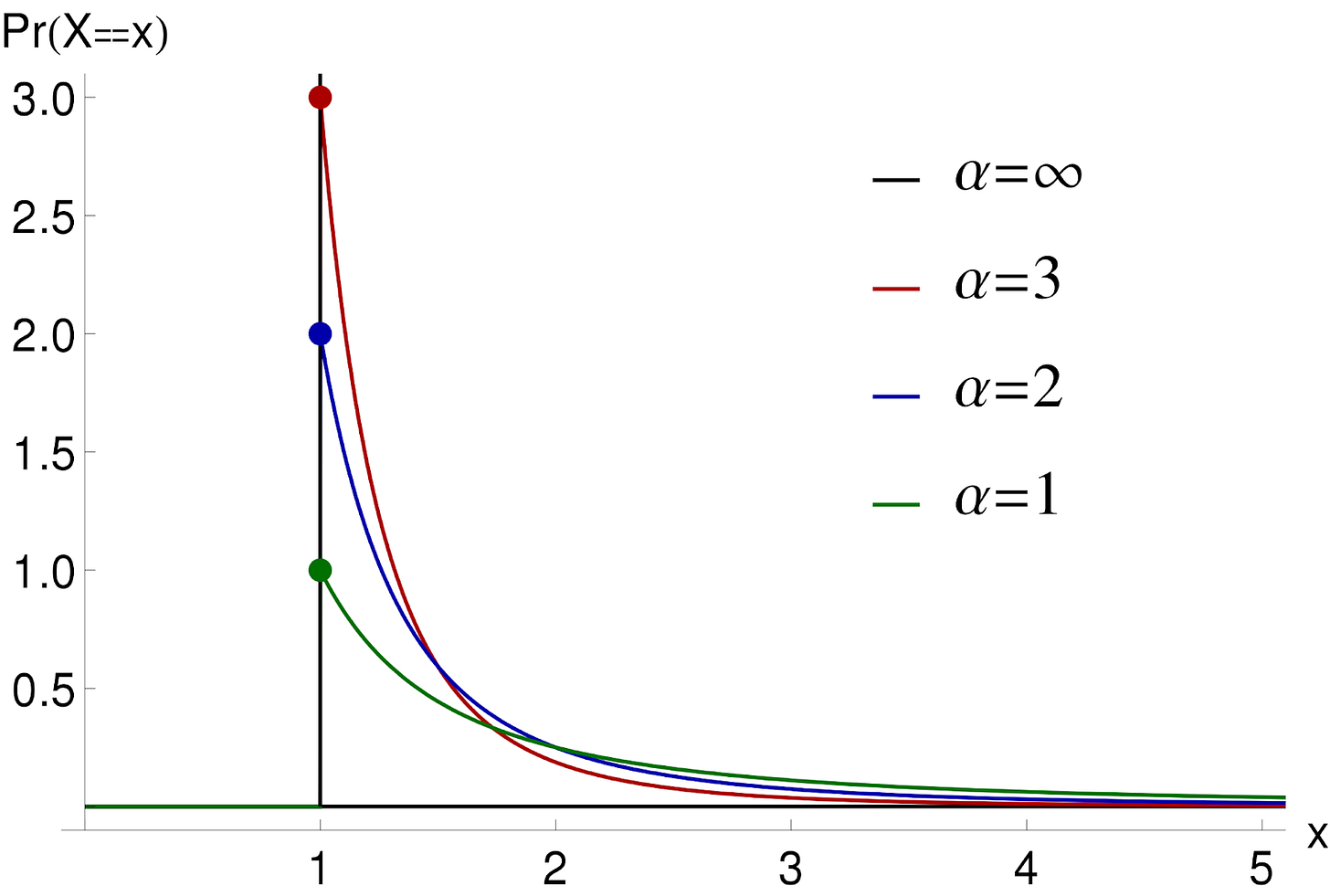
Inverse power laws (and their inverse, power laws) appear all over the place.
One place they've been noticed quite a bit is in the business world, where people often talk about the Pareto Principle: 20% of the work generates 80% of the profit. 20% of clients generate 80% of sales. 20% of bugs generate 80% of errors in software. 20% of web content generates 80% of traffic.
This 80-20 rule is often a rallying cry to focus on the impactful stuff in the business world. Beyond that you get diminishing returns. This is easier said than done, since in a business context you often don't know what 20% will drive things, so it sort of turns into the trite advice to "do the important stuff, don't waste time on the unimportant stuff". But there needs to be some content to fill those business advice columns, so the 80-20 rule lives on.
But this 80-20 rule doesn't just apply to businessy stuff. The rule originally came from an Italian engineer, Vilfredo Pareto, observing that 20% of the population owned 80% of the land in Italy.
There's no mathematical reason for the numbers to be 80 and 20, and in reality, they often aren't. It's just a rule of thumb. Like you can see in the figure above, you can have steeper or shallower drop-offs. But the phenomenon of a small amount accounting for an outsized proportion of an outcome is very common.
An extreme proportion comes from the 1% rule, which states that 1% of an online community creates all of the content (while everyone else lurks). This has actually been empirically tested, and at least in the digital health forums investigated, the top 1% of users created 75% of the content. The bottom 90%, the lurkers, created about 1% of the content.
Don't want to be a lurker? Join the 1% by commenting
Another example, though it's harder to empirically validate, is Sturgeon's law. Theodore Sturgeon was a science fiction writer who was frustrated defending science fiction from its critics—it seemed there was so much crappy science fiction to point at giving the snobs ammunition. Sturgeon realized a lot of science fiction was crap, but that a lot of basically everything is crap. Thus, Sturgeon's law:
90% of everything is crap
—Sturgeon's Law
Presumably this means the remaining 10% is not crap, and therefore 10% of science fiction (or of anything else) accounts for an outsized portion of the quality.
Why do we see so many situations where a small proportion of causes creates a much larger proportion of the outcomes?
I don't think there's a single overarching reason. In some cases above, there is some logic that creates a nonlinear relationship—Pareto's original observation about the distribution of land is likely because it's easier for the rich to get richer. If you have a bit of wealth, the wealth can work for you (investments), creating more.
But in other cases it's just that some stuff is much more common or important than others. A small proportion of bugs creating an outsized portion of the errors makes perfect sense—some code is more central to the experience of users and therefore executes more, resulting in lots of errors if there is a bug in it.
Taking the obvious into account
Working as a data scientist, there's been a pattern I've noticed: people think that, deep within the data, there is some secret pattern.
A lot of prediction problems have really obvious predictors. For one thing, the past is an absurdly good predictor of the future. Want to know who is most likely to return their library book late? Those who have returned it late in the past. A couple of real examples from my professional work: Which of our patients are likely to have a poor health outcome? Those that have had that poor outcome before. Which health insurance claims are likely to be denied by the payer? Those going to a payer that denies a lot of claims.
Management likes to brag about their complex machine learning models that contain thousands of factors, and I've again and again been encouraged to build big, complex models. And again and again, I've found only a small handful of the variables matter. And they tend to be the ones any subject matter expert would have pointed you to.
Yes, there are lots of small factors and complex relationships deep in the data. But almost always, just getting the obvious stuff gives you nearly all the predictive power you're going to get. There's a very steep drop-off in the usefulness of any data after that—it's extremely uncommon for there to be some deep secret pattern buried in the interactions between two variables you never would have thought of.
In human decision-making, there's evidence of a "less is more" effect, where more accurate decisions are made when fewer factors are considered. In some domains, increasing expertise leads to using heuristics that rely on very little information, like the Take-The-Best heuristic, where you consider the most important factors first and make your decision based on the first factor you find that distinguishes the options under consideration.
It's often smart to ignore the small factors, they're just a distraction.
Keep it simple, stupid
Let's talk about Buridan's ass. 😏
Buridan was a 14th century French philosopher. I'm not sure if he was known for having junk in his trunk, but he was famous for his moral philosophy.
One idea he was known for was that if there were two equally good options, a decision could not rationally be made, so he suggested one should suspend judgment until the choice is clear.
Other writers satirized this with the idea of a donkey (yes, that kind of ass, sicko) that was equally thirsty and hungry. Standing between a pail of water and a bale of hay, Buridan's ass, with two equally good options, wouldn't be able to choose between them and die of starvation and thirst.
There's an obvious solution to the ass's problem: flip a coin (a mental one, since asses don't have opposable thumbs).
We humans often act like asses. When faced with a hard decision, we'll spend a lot of time and energy trying to decide between two options. The funny thing is, if we're having so much trouble with the decision, that must mean the options aren't much better or worse than each other—if they were, it would be easy to just pick the better one.
Ironically, this means the choices we spend the most time on are the ones where what we choose matters the least—if the difference between how much we value each of the options is so small that there isn't an obvious choice, we don't lose out on much by choosing an option that might have, after more consideration, turned out to be the second-best.
This is sometimes referred to as Fredkin's Paradox:
The more equally attractive two alternatives seem, the harder it can be to choose between them—no matter that, to the same degree, the choice can only matter less.
—Edward Fredkin
So maybe we should fret less about our decisions—the long tail of possible factors isn't likely to matter, but the time we waste and anxiety we experience from prolonging the decision might.
Please hit the ❤️ “Like” button below if you enjoyed this post, it helps others find this article.
If you’re a Substack writer and have been enjoying Cognitive Wonderland, consider adding it to your recommendations. I really appreciate the support.




This makes me think about science in general, in which researchers are encouraged to generate theories that contain lots of complicated factors, but may not lead to results outside the lab. My cognitive distortions are telling me that this means that all researchers are basically over analyzing the data, with the same fervor as severely anxious people do, to uncover the results that confirm their biases toward getting a particular outcome. This makes me question the reliability and usefulness of theoretical work in general, but what do you think?
it's brilliant how you explain stuff so easily. you're a great writer