Thinking in Distributions
Noisy trends and counter-examples show why we should practice epistemic humility
This is a post about epistemology disguised as a statistics lesson. Now that I have you really hyped, let's do this.
While I was doing my PhD, an undergrad in the lab brought up a recent news headline. It claimed that being mentioned on social media causes research papers to be cited more. The undergrad was indignant at the idea—he didn’t believe serious scientists found out about research on Twitter. My PhD advisor just shrugged and asked, “How big is the effect size?”
A special transformation had taken place here. My advisor had transformed a hard fact about the world ("social media increases citations") into a softer, more nuanced question ("how much does social media impact citations?").
My thesis here has two parts. One, many things we know about the world are better taken as soft trends rather than hard logical necessities. Two, we simplify these soft trends to communicate, and this activates a rule-based way of thinking about the world that often distorts both the importance of and the level of certainty we have about the trend. This is an ode to thinking in distributions and epistemic humility.
Rules and Counter-Examples
Whenever there's a science headline with some clickbaity title like: “Eldest siblings are more intelligent”, I always cringe at the inevitable comments: “I’m the youngest, and I’m definitely smarter than my brothers!”, “That’s not always true! My middle-child is the genius of the family”, or the self-serving “Yep, I’m the oldest and I can confirm this!” Some of these comments are joking, but always with an underlying sense that they’ve vanquished (or confirmed) this scientific finding.
These people have interpreted the headline as a rule: “older siblings are always more intelligent than younger ones”. You can hardly blame them, headlines are generally framed as hard statements of fact, not nuanced statements of trends. A single counterexample disproves the headline. Checkmate, scientists.
But even for incredibly strong effects, there are usually at least some examples that go against the norm. Take, for example, male vs female grip strength. It's generally known that males have more upper body strength than females. The research bears this out, and the size of the difference is huge—median female grip strength is about 64% the median grip strength of males. Look at this plot from
over at :The regions where the red and blue overlap show where you would find males weaker than females. You can see there are some males weaker than the median female (any of the overlap region to the left of the vertical red line). This makes sense—this sample is representative of the US population, so it includes the elderly, people with arthritis, and people with disabilities. You even find some females that have a stronger grip strength than the median male (the small bit of overlap to the right of the blue line)—not many, only about 0.1% of females, but they exist.
Even with an enormous effect size, you often still have data points that go against the trend. When we get into weaker effects, this is much more true.
Effect sizes
Going back to the social media citation study, someone with a more rules-based perception would think any time a paper gets mentioned in Twitter, it’s guaranteed to be in a different echelon in terms of citations. A more statistically sophisticated view is that there is some non-zero effect of social media, but it could be tiny. Measure enough examples, and you can detect a small effect—even if being mentioned on Twitter only results in an average increase of 0.1 citations, if it’s non-zero, it’s measurable.
The thing is, almost every effect is non-zero. If there’s even a remotely plausible link between two things, there’s almost certainly a non-zero statistical relationship. Scientists typically use statistical testing to see if two distributions are different. With a large enough sample size, the tiniest effects will be "statistically significant". But an effect can be statistically significant while being so small it's meaningless for practical purposes.
Noisy Signals
Noise is a statistical term used to describe unexplained variability in data. It comes from signal processing, where electromagnetic radiation degrades the signals being transmitted over a line, literally creating noise for things like telephone calls.
In different fields, we expect different levels of noise. In physics, effects are extremely well characterized, so they expect very low levels of noise. They might still get some, but it's because of either measurement error (limitations of whatever device we are using to measure the outcome of an experiment) or stuff like quantum fluctuations (inherent randomness in the universe).
The social sciences are another matter:
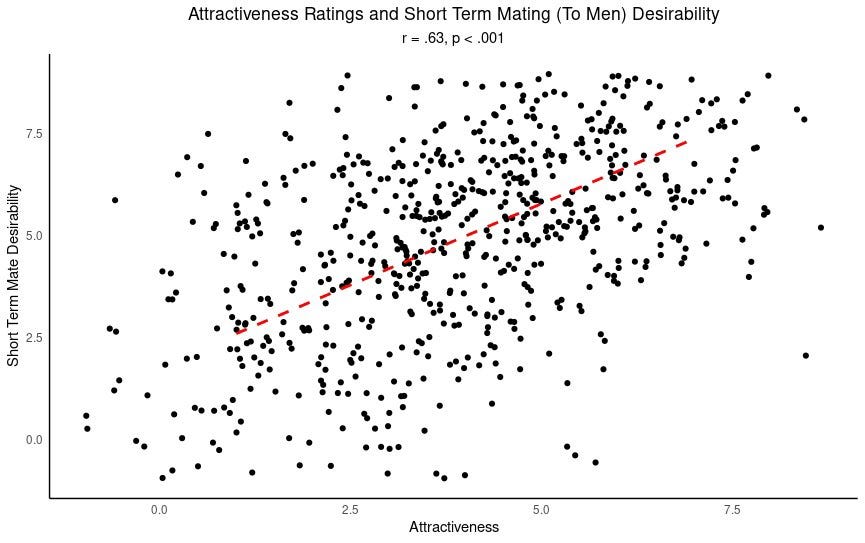
Siberian fox is not making this up. Here is the plot they are referring to, showing "short term mate desirability" ratings compared to "attractiveness ratings", according to men shown a photo of a woman:
In this plot, each point is a picture that was rated by men on attractiveness and "short-term mate desirability" (how much they want to have a one-night stand). To be clear, this is a really strong, clear effect—for the social sciences. But look at the spread of the points. It's noisy!
You have points in the top left that were rated low in attractiveness but high in short-term mate desirability. In the bottom right are points rated attractive that men have low desire for "short term mating" with. There is a greater density of points going along the diagonal, showing the trend we expect: short-term mating desirability tends to go up when attractiveness goes up.
The attractiveness ratings explain surprisingly little of the variance. We can quantify that—the r2 value for this relationship is just under 40%, which is the measure of "how much variability is explained". So attractiveness only explains about 40% of how much men desire a one-night stand even if that desire is based entirely on a picture.
In the social sciences it's common to have much weaker effects that explain tiny portions of the variance in behavior. Not that we should dismiss the social sciences. I think the better interpretation is that human behavior is complex, so any isolated effect on behavior is bound to be limited in what it explains. We should be careful when we hear confident statements of universal truths about human behavior (and hold at arm's-length our own beliefs about how people act).
Weak effects aren't the sole domain of the social sciences. To grab one example, here is a figure from a study that is cited (e.g. here and here) as a source on the link between caffeine and poor sleep quality:
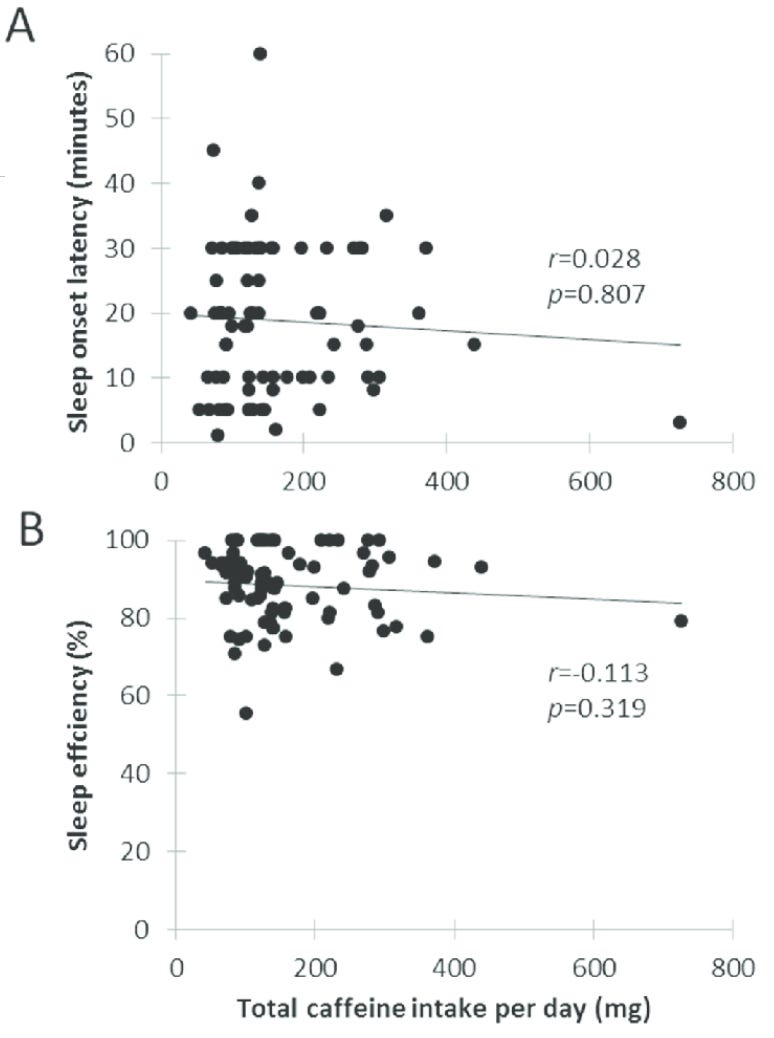
There almost certainly is a link between caffeine consumption and sleep quality. But lots of other things affect sleep quality as well, and the effect of caffeine isn't so strong that the signal becomes clear looking at even dozens of examples. For any individual, the effect of caffeine might be negligible compared to other things affecting their sleep (stress from work, poor sleep hygiene, poor sleeping conditions, etc.), and plenty of people consume substantial amounts of caffeine while being able to sleep well.
So does caffeine impact sleep quality? According to meta-analyses (analysis that looks across a bunch of studies looking at this), yes. The effect is there. It's just a relatively small signal amidst a lot of noise, to the point where any individual study might not even find the link. It also, of course, matters when you consume caffeine—there's more robust evidence that if you consume caffeine close to bedtime, you'll have worse sleep.
If you're having trouble sleeping, cutting out caffeine makes sense (and is likely the advice you'll get from a doctor). But it doesn't mean everyone who has a lot of caffeine has trouble sleeping, or that everyone who has trouble sleeping drinks a lot of caffeine.
The trees for the forest
The headlines and statements we get about scientific studies, especially in the social sciences, should be taken as (often weak) overall group trends, not never-broken rules. They explain a small portion of the complexity of human behavior.
Despite all the noise in signals we care about, we can still make true statements about them. It's true that "men prefer one-night stands with attractive women" and "caffeine has a negative impact on sleep quality". But note how much information we lose when we boil everything down to those statements. We throw away everything we know about how variable and noisy those trends are in exchange for a simple statement that there is a trend. When we go from looking at the trees to looking at the forest, we talk in terms of rules, not distributions.
But we have to boil down our uncertain knowledge so we can communicate. Health agencies and medical professionals need to give guidance based on often noisy health science research. Business analysts need to give guidance on noisy data to leaders who make decisions. And in everyday life, we have to talk about personality traits individuals have based on limited observations of their behavior (because otherwise what would we gossip about?).
There's a broader point here that I'll have to flesh out in later posts, but let me tease it here: Much of our knowledge is of this form, where we start with messy data and translate that into a factual statement that loses nuance. Even the concepts we use to carve up and understand the world are built up from noisy data. We learn concepts over time through seeing lots of examples, not by being given a strict definition. The concept of chair, for example, is really hard to give a definition of:
I think most (if not all) of our concepts are like this. What is knowledge? If you think you can define it, take a moment to appreciate that epistemologists have been arguing about this a long time, and it turns out definitions like "justified, true belief" have counterexamples.
Our concepts are built up out of exposure to noisy examples. It's therefore difficult to articulate their exact definitions and the concepts themselves often break down at the edges. This doesn't mean they aren't useful, but it does mean we should be careful about taking them too seriously as metaphysical facts of the universe.
One of my frustrations with much of analytical philosophy is how often it relies on hard, precise definitions and rules. This leads to arguments about concepts where a single counterexample upends a philosophical theory, leading to a new theory, which is upended by another single counterexample. Peter Unger has pointed out this cycle and argued that much of modern philosophy is just "Empty Ideas" because it's arguing about definitions that don't really matter. I'm not quite that pessimistic, but I think there's a lot to say about that as a critique (and I'm sure I'll be saying more about it in the future).
For now, let's just try to appreciate that our knowledge often relies on messy data, and try to do more thinking in distributions. It's a good way to practice some epistemic humility.
If you enjoyed this post, consider sharing it. You can also help others find it by hitting the heart button to “Like” the post.
If you’re a Substack writer and have been enjoying Cognitive Wonderland, consider adding it to your recommendations. I really appreciate the support.







I keep trying to explain these things to my psychiatrist. I’m not sure why an actual doctor has so much trouble understanding that his patients are beautiful, unique snowflakes ( 😆 ) who might not be able to be satisfactorily flattened into a single DSM diagnosis (I’m a horse, not a chair!), who might not be able to enjoy the headline-level certainty that his prescription will work, or who fall outside the probability curve on a “very rare” side effect.
What I’m saying isn’t “checkmate scientists”—I have no doubt that psychiatry often works exactly as intended—it’s just frustration that my doctors so often categorically state that something unusual “can’t” be happening.
I guess they have to overcorrect for people using Dr Google and who make all of these errors… but it does nothing for my faith and trust in a profession that I desperately depend on for stable, healthy integration with society.
Holy wow could we somehow make it obligatory for the entire internet to read and internalize this. I feel it might significantly improve quality of average online debate.